3. Indifference Curves Cannot Intersect
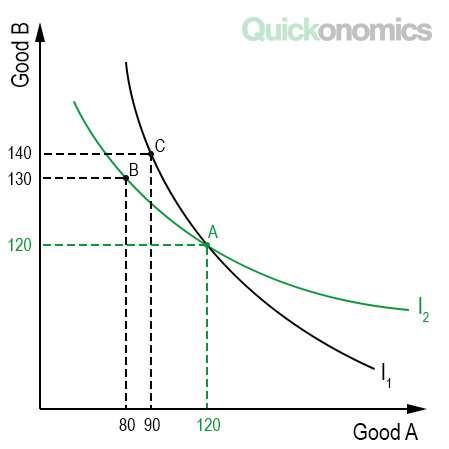
Two indifference curves can’t cross. To understand why this is the case, we can look at what would happen if they did intersect. As we know, all combinations of good A and good B that lie on the same indifference curve make the consumer equally happy. Therefore, if two indifference curves were to cross, they would both have to provide the consumer with the same level of total satisfaction, because the exact point where they intersect (i.e., point A) is on both curves. Thus, all other combinations on both curves would have to provide the same level of satisfaction as well. However, if we compare point B and point C, we can see that point C offers more of good A and good B (90 and 140) as compared to point B (80 and 130). As we already learned above, consumers always prefer larger quantities. Therefore both curves can’t provide the same level of satisfaction, which means they can never intersect.
4. Indifference Curves are convex (i.e., bowed inward)
In most cases, indifference curves are bowed inward. This has to do with the marginal rate of substitution (MRS). We know that the marginal utility of consuming a good decreases as its supply increases (see also diminishing marginal utility). Therefore consumers are willing to give up more of this good to get another good of which they have little. Let’s look at the graph below to illustrate this. If a consumer has a lot of good B, the MRS is 3 units of good B per unit of good A. If she has more of good A, the MRS is 0.5 units of good B per unit of good A. In other words, if they have a lot of good B, they are more willing to trade some of it in to get an additional unit of good A and vice versa. Because of this relationship, the indifference curve is bowed inward (i.e., convex).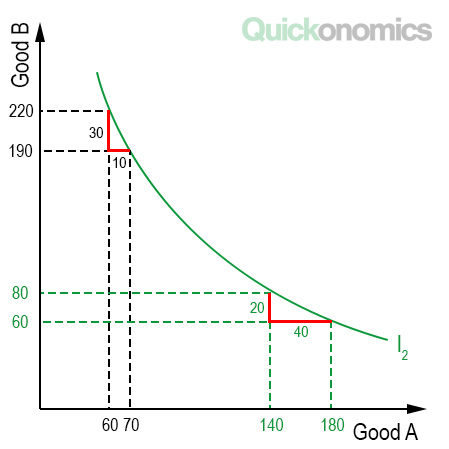
In a Nutshell
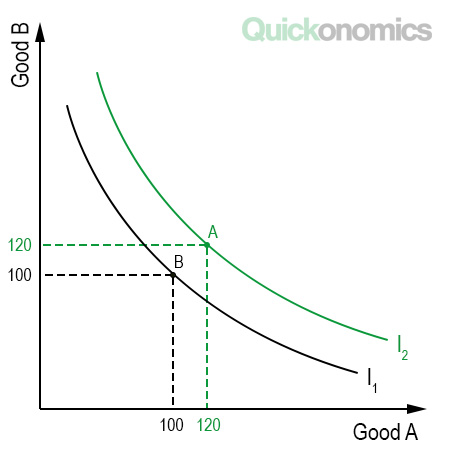
Indifference curves are graphical representations of various combinations of two commodities which an individual considers equally valuable. They are used to analyze consumer preferences and a number of other concepts. There are four important properties of indifference curves that describe most of them: (1) They are downward sloping, (2) higher indifference curves are preferred to lower ones, (3) they cannot intersect, and (4) indifference curves are convex (i.e. bowed inward).