How to Calculate Price Elasticities Using the Midpoint Formula

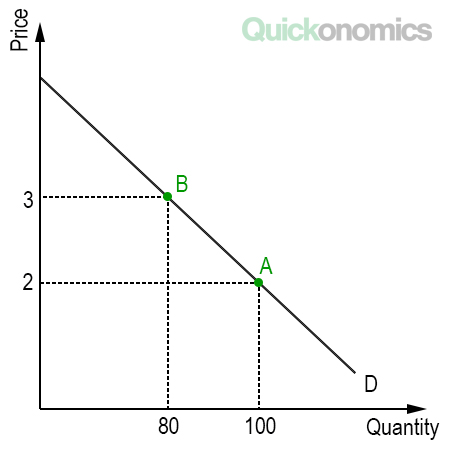
Updated Feb 28, 2024

Price elasticity of demand is a measure that shows how much quantity demanded changes in response to a change in price. It is calculated as the percentage change in quantity demanded divided by the percentage change in price (see also Elasticity of Demand). However, as you will notice sooner or later, this method has an annoying limitation: It will not produce distinct results when we use it to calculate the price elasticity of two different points on a demand curve (i.e., arc elasticity).

Fortunately, there is a simple trick we can use to avoid this issue: the so-called midpoint method to calculate elasticities. Thus, in the following paragraphs, we will learn step-by-step how to use the midpoint formula to calculate price elasticities. But before we do that, let’s take a step back and look at why the issue we mentioned above arises in the first place.

Elasticity Between Two Points on a Curve

When we try to calculate the price elasticity of demand between two points on a demand curve as described above, we quickly see that the elasticity from point A to point B seems different from the elasticity from point B to point A. While this seems odd at first, it makes perfect sense because we generally calculate percentage changes relative to their initial value. Now, if we move from point A to point B, the initial value is at level A. However, if we move from point B to point A, the initial value is at level B. To illustrate this, let’s look at the graph below.

As you can see, at point A, the initial price is USD 2.00, and the quantity is 100 units. Meanwhile, at point B, price and quantity are USD 3.00 and 80 units, respectively. That means, going from point A to point B, the price increases by 50% (i.e. [3-2]/2) while quantity decreases by 20% (i.e. [80-100]/100). This indicates a price elasticity of 0.4 (i.e., 20/50). By contrast, going from point B to point A, the price only decreases by 33% (i.e. [2-3]/3) while quantity increases by 25% ([100-80]/80). This indicates a price elasticity of 0.75 (i.e., 25/33).

The Midpoint Formula

As mentioned before, we can avoid this problem by using the so-called midpoint method. Usually, when we calculate percentage changes, we divide the change by the initial value and multiply the result by 100. Unlike that, the midpoint formula divides the change by the average value (i.e., the midpoint) of the initial and final value.

In the case of our example (see above) the average price is USD 2.50 (i.e. [2.00 + 3.00]/2) and the average quantity demanded is 90 (i.e. [100 + 80]/2). Thus, according to the midpoint method, a change from point A to point B (i.e. USD 2.00 to 3.00) is considered a 40% increase (i.e. [3.00 – 2.00]/2.50). Similarly, a change from point B to point A (i.e., USD 3.00 to 2.00) is considered a 40% decrease (i.e. [2.00 – 3.00]/2.50).

As you can see, the percentage change is the same regardless of the direction we move. Of course, this also holds for the quantity demanded. A move from point A to point B (i.e. 100 to 80) is considered a 22% decrease (i.e. [80 – 100]/90). Similarly, a move from point B to point A (i.e., 80 to 100) is considered a 22% increase ([100 – 80]/90).

By using the percentage changes calculated with the midpoint method, we can now compute a distinct price elasticity of demand between points A and B. To do this, we use the following formula:

The formula looks a lot more complicated than it is. All we need to do at this point is divide the percentage change in quantity demanded we calculated above by the percentage price change. As a result, the price elasticity of demand equals 0.55 (i.e., 22/40).

Please note: Unless stated otherwise, it is advisable to use the midpoint method whenever you have to calculate percentage changes and price elasticities between two points on a curve.

Frequently Asked Questions (FAQs)

How does the midpoint formula compare to other methods of calculating price elasticity in terms of accuracy and applicability in different economic scenarios?

The midpoint formula is appreciated for its simplicity and unbiased approach, averaging percentage changes in price and quantity to calculate elasticity. It differs from methods like point elasticity, which is more precise for specific data points but less generalizable across different scenarios. The midpoint formula’s balanced calculation makes it broadly applicable, avoiding skew towards initial or final values, which can be a limitation in other methods.

Can the midpoint formula be applied to calculate other types of elasticities, such as income elasticity of demand or cross-price elasticity of demand?

Yes, the midpoint formula can theoretically be applied to calculate other types of elasticities, such as income elasticity of demand or cross-price elasticity of demand. This would involve adjusting the variables used in the formula to reflect the change in income or the price of another good, respectively, instead of the price change of a single good. It showcases the formula’s flexibility and potential for broader economic analysis.

What are the limitations or potential drawbacks of using the midpoint formula for calculating price elasticity in real-world economic analysis?

The limitations of the midpoint formula mainly arise in situations involving large changes in price or quantity, where the formula might not accurately reflect the elasticity of demand. While beneficial for ease of understanding and application, its simplicity may not capture the complexity of consumer behavior in more volatile markets. This suggests the formula is best used within certain boundaries, where changes are moderate, and the demand curve does not exhibit extreme sensitivity.

Summary

Price elasticity of demand shows how much quantity demanded changes in response to a change in price. It can be calculated as the percentage change in quantity demanded divided by the percentage change in price. However, this method does not produce distinct results when we use it to calculate the price elasticity of two different points on a demand curve (i.e., results are different based on the direction of change). To fix this, the midpoint formula computes percentage changes by dividing the change by the average value (i.e., the midpoint) of the initial and final number. As a result, it produces the same result regardless of the direction of change. Therefore is advisable to use the midpoint method whenever you calculate percentage changes and price elasticities between two points on a curve.